二叉树知识锦囊（二）-创新互联

作者：爱塔居

成都创新互联是一家专业提供寿宁企业网站建设,专注与成都网站设计、网站制作、成都h5网站建设、小程序制作等业务。10年已为寿宁众多企业、政府机构等服务。创新互联专业网站设计公司优惠进行中。

专栏：数据结构

作者简介：大三学生，希望和大家一起进步！

文章目录

文章目录

一、二叉树的存储

二、二叉树的遍历（重点）

2.1 前序遍历

2.2 中序遍历

2.3 后序遍历

2.4 层序遍历

2.5 小题实练

三、代码实现

---

一、二叉树的存储

二叉树的存储结构分为：顺序存储和类似于链表的链式存储。

二叉树的链式存储是通过一个一个的节点引用起来的，常见的表示方式有二叉和三叉表示方法。

二、二叉树的遍历（重点）

遍历是指沿着某条搜索路线，依次对树中的每个节点，均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。

2.1 前序遍历

前序遍历：根结点》左子树》右子树

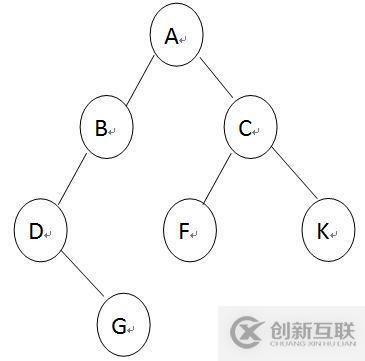
前序遍历：

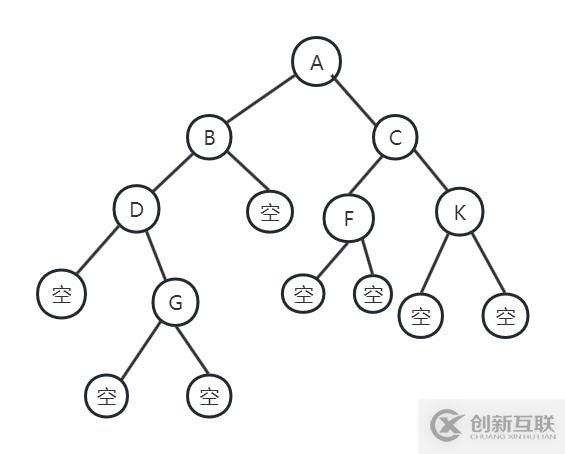
从A开始，打印A往左走，遍历到B，打印B,再遍历B的左子树D，打印D，接着遍历D的左子树，发现为空，返回D，再遍历D的右子树G，打印G，遍历G的左右子树都为空，返回G,返回D，返回B，遍历B的右子树为空，返回B，返回A。

再遍历A的右子树C，打印C，遍历C的左子树F，打印F，再遍历F的左右子树为空，返回F，返回C，再遍历C的右子树K，打印K,遍历K的左右子树为空，返回K，返回C，返回A。

所以这个二叉树的前序遍历为

2.2 中序遍历

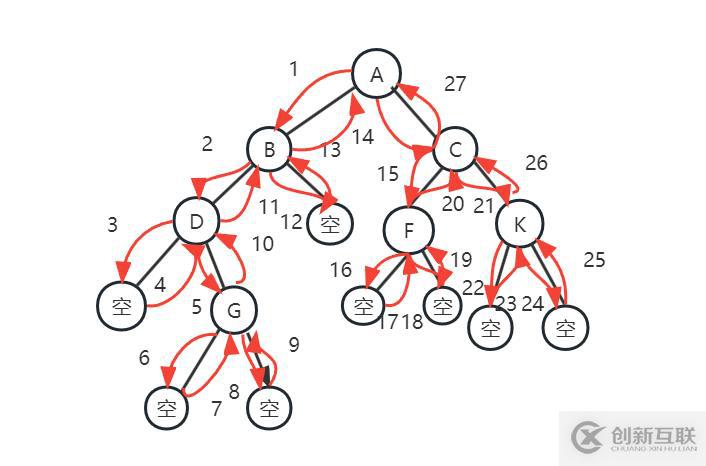
中序遍历：左子树》根》右子树

从A开始，到A的左子树B，遍历B的左子树D，遍历D的左子树为空，返回D，打印D，遍历D的右子树G，遍历G的左子树为空，返回G，打印G，遍历G的右子树为空，返回G，返回D，返回B，打印B,遍历B的右子树为空，返回B，返回A，打印A。

再遍历A的右子树C，遍历C的左子树F，遍历F的左子树为空，返回F，打印F，遍历F的右子树为空，返回F，返回C，打印C，遍历C的右子树K，遍历K的左子树为空，返回K，打印K，遍历K的右子树为空，返回K，返回C，返回A。

故该二叉树的中序遍历为

2.3 后序遍历

后序遍历：左子树》右子树》根 

从A开始，遍历A的左子树B，遍历B的左子树D，遍历D的左子树为空，返回D，遍历D的右子树G，遍历G的左右子树为空，返回G，打印G,返回D，打印D，返回B，遍历B的右子树为空，返回B，打印B ，返回A。

遍历A的右子树C，遍历C的左子树F，遍历F的左右子树为空，返回F，打印F,返回C，遍历C的右子树K，遍历K的左右子树为空，返回K，打印K，返回C，打印C，返回A，打印A。

故该二叉树的后序遍历为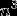

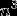
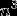
2.4 层序遍历

层序遍历就是自上而下，自左至右访问树的结点的过程。

这个二叉树的层序遍历为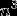

2.5 小题实练

1.某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA

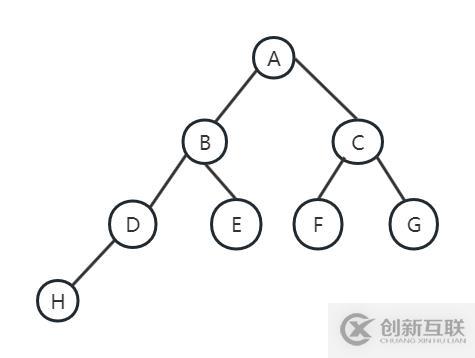
因为是完全二叉树，所以我们根据层序遍历的结果可以画出二叉树：

根据二叉树，我们得出前序遍历结果ABDHECFG

2.二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：HFIEJKG.则二叉树根结点为()
A: E B: F C: G D: H

先序遍历第一个结点就是根结点，故为A；

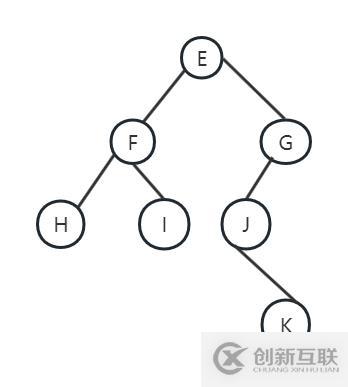
如果这道题要我们画出这个二叉树，我们也可以画出：

因为中序遍历顺序，根结点的左边结点都是在左边，右边的结点都是在右边。

3.设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历序列为()
A: adbce B: decab C: debac D: abcde

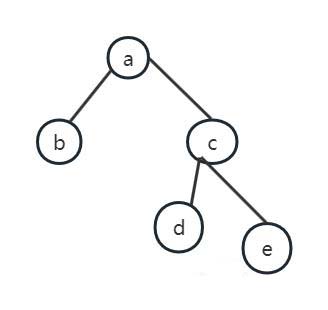
根据中序遍历和后序遍历结果画出二叉树图为：

前序遍历结果：abcde

4.某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出(同一层从左到右)的序列为()
A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF

层序遍历结果：FEDCBA

🍓那如果知道前序遍历序列和后序遍历序列，我们可以画出二叉树吗？

答案是不行。因为这样，我们只能找到根结点，不能确定左子树和右子树的位置。

三、代码实现

接下来，我们尝试着创建一个二叉树。

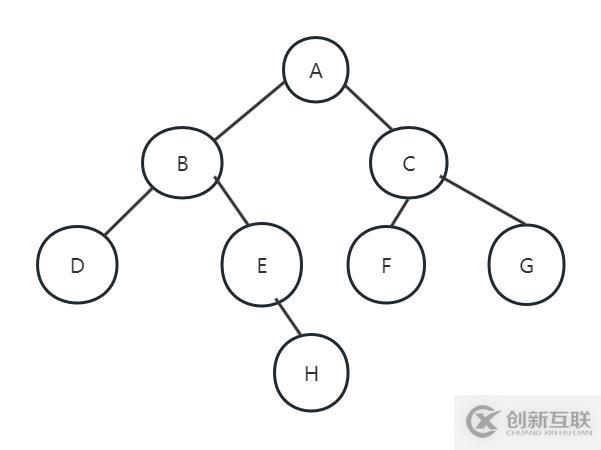
public  class TestBinaryTree {
static  class  TreeNode {
    public char val;//数据域
    public TreeNode left;//左孩子节点
    public TreeNode right;//右孩子节点
    public TreeNode(char val) {
        this.val = val;
    }
}
    public TreeNode createTree( ){
        TreeNode A=new TreeNode('A');
        TreeNode B=new TreeNode('B');
        TreeNode C=new TreeNode('C');
        TreeNode D=new TreeNode('D');
        TreeNode E=new TreeNode('E');
        TreeNode F=new TreeNode('F');
        TreeNode G=new TreeNode('G');
        TreeNode H=new TreeNode('H');
        A.left=B;
        A.right=C;
        B.left=D;
        B.right=E;
        C.left=F;
        C.right=G;
        E.right=H;
        return A;
    }

先序遍历：

public void preOrder(TreeNode root){
        //当二叉树根结点为空
    if(root==null){
        return;
    }
    //不为空，打印树的根结点的值
    System.out.print(root.val+" ");
    //这时对左子树进行先序遍历，又是新的二叉树
    preOrder(root.left);
    preOrder(root.right);
}

中序遍历：

void inOrder(TreeNode root){
        if(root==null){
    return;
}
        inOrder(root.left);
    System.out.print(root.val+" ");
        inOrder(root.right);
}

后序遍历：

void postOrder(TreeNode root){
    if(root==null){
        return;
    }
    inOrder(root.left);
    inOrder(root.right);
    System.out.print(root.val+" ");
}

完整代码见链接：javacode: java的日常代码---------------------- - Gitee.com 

你是否还在寻找稳定的海外服务器提供商？创新互联www.cdcxhl.cn海外机房具备T级流量清洗系统配攻击溯源，准确流量调度确保服务器高可用性，企业级服务器适合批量采购，新人活动首月15元起，快前往官网查看详情吧

当前名称：二叉树知识锦囊（二）-创新互联
链接URL：https://www.cdcxhl.com/article48/cciihp.html

成都网站建设公司_创新互联，为您提供小程序开发、服务器托管、网站维护、手机网站建设、云服务器、App设计

广告

声明：本网站发布的内容（图片、视频和文字）以用户投稿、用户转载内容为主，如果涉及侵权请尽快告知，我们将会在第一时间删除。文章观点不代表本网站立场，如需处理请联系客服。电话：028-86922220；邮箱：631063699@qq.com。内容未经允许不得转载，或转载时需注明来源： 创新互联