二叉树常考面试题-创新互联
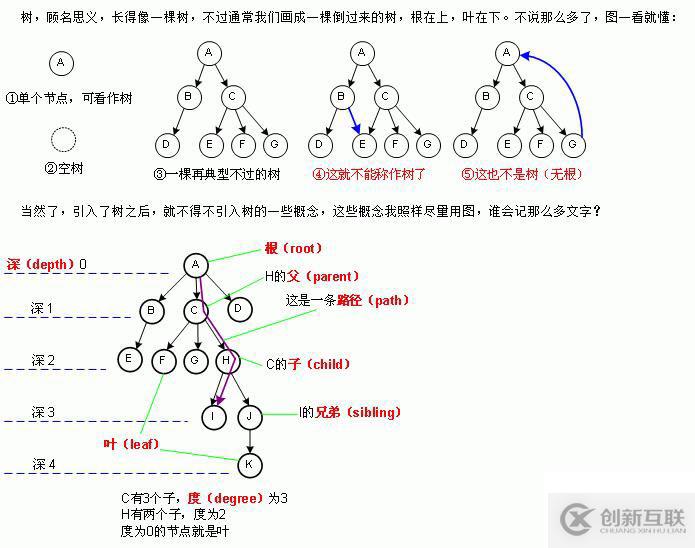
树相关的一些概念。
目前成都创新互联已为上千的企业提供了网站建设、域名、网络空间、网站托管、服务器租用、企业网站设计、洪湖网站维护等服务,公司将坚持客户导向、应用为本的策略,正道将秉承"和谐、参与、激情"的文化,与客户和合作伙伴齐心协力一起成长,共同发展。
树是n(n>=0)个有限个数据的元素集合,形状像一颗倒过来的树。
结点:结点包含数据和指向其它结点的指针。
结点的度:结点拥有的子节点个数。
叶子节点:没有子节点的节点(度为0)。
父子节点:一个节点father指向另一个节点child,则child为孩子节点,father为父亲结点。
兄弟节点:具有相同父节点的节点互为兄弟节点。
节点的祖先:从根节点开始到该节点所经的所有节点都可以称为该节点的祖先。
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
树的高度:树中距离根节点最远结点的路径长度。
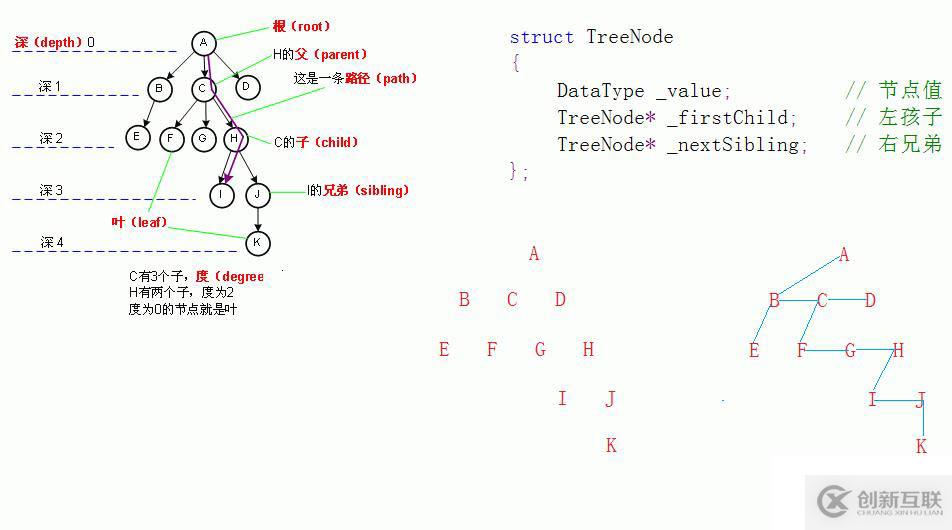
树的存储结构:
二叉树的结构
二叉树:二叉树是一棵特殊的树,二叉树每个节点最多有两个孩子结点,分别称为左孩子和右孩子。
满二叉树:高度为N的满二叉树有2^N - 1个节点的二叉树。
完全二叉树 若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树
前序遍历(先根遍历):
(1):先访问根节点;
(2):前序访问左子树;
(3):前序访问右子树;
中序遍历:
(1):中序访问左子树
(2):访问根节点;
(3):中序访问右子树;
后序遍历(后根遍历):
(1):后序访问左子树;
(2):后序访问右子树;
(3):访问根节点;
层序遍历:
(1):一层层节点依次遍历。
下面是二叉树的具体实现:
template<class T>
struct BinaryTreeNode
{
BinaryTreeNode<T > *_left;
BinaryTreeNode<T > *_right;
T _data;
};
template<class T>
class BinaryTree
{
Typedef BinaryTreeNode< T> Node;
protected:
Node *_root;
public:
BinaryTree() //无参构造函数
:_root( NULL)
{
}
BinaryTree( const T *a, size_t size, const T& invalid)
{
size_t index = 0;
_root = _CreateTree( a, size , invalid, index);
}
protected:
Node *__CreateTree( const T *a, size_t size, const T& invalid, size_t &index )
{
Node *root = NULL;
if (index < size && a[index ] != invalid) //是有效值时
{
root = new Node(a [index]);
root->_left = __CreateTree( a, size , invalid, ++ index);
root->_right = __CreateTree( a, size , invalid, ++index);
}
return root;
}
//前序遍历--------递归写法,缺点是:有大量的压栈开销。
void Prevorder(Node *root )
{
if (root == NULL)
{
return;
}
else
{
cout << root->_data << " " ;
_prevorder( root->_left);
_prevorder( root->_right);
}
}
//前序遍历------------非递归写法
//前序遍历的非递归写法思想:需要借助栈。
void PrevOrderRonR()
{
stack<Node*> s;
if (_root == NULL )//根结点为空的话直接return掉即可。
{
return;
}
if (_root)
{
s.push(_root); //根不为空的时候将根结点进行压栈。
}
while (!s.empty())//判断栈是否为空
{
Node *top = s.top(); //栈不为空,则取栈顶元素
cout << top->_data << " ";//然后进行访问栈顶元素
s.pop(); //访问完栈顶元素将其从栈中pop掉。
if (top->_right)//要根据栈进行先序遍历,则必须是先访问根节点,再访问左子树,最后访问右子树,因为栈是“后进先出的”,要想先访问左子树,则必须先入右子树,再入左子树。如果栈顶元素的右子树不为空,
{
s.push(top->_right); //栈顶的右子树不为空,将其进行压栈。
}
if (top->_left)
{
s.push(top->_left); //栈顶的左子树不为空,将其进行压栈。
}
}
cout << endl;
}
//中序遍历----------递归写法
void _Inorder(Node *root )
{
if (root == NULL)
{
return;
}
else
{
_Inorder(Node * root)
{
if (root == NULL )
{
return;
}
else
{
_Inorder(root->_left);
cout << root->_data << " " ;
Inorder(root->_right);
}
}
}
}
//中序遍历的非递归写法,思想是:也是借助栈,主要核心是找最左结点,定义一个cur指针,让它最开始指向_root。
void TnOrderNonR()
{
stack<Node*> s;
Node *cur = _root;
while (cur || !s.empty())
{
whie(cur) //找最左结点
{
s.push(cur); //将cur压栈。
cur = cur->_left; //cur指向它的左孩子
}
Node *top = s.top();
cout << top->_data << " ";
s.pop();
cur = top->_right;
}
}
//后序遍历---------递归写法
void Postorder(Node *root )
{
if (root == NULL)
{
return;
}
else
{
Postorder( root->_left);
Postorder( root->_right);
cout << root->_data << " " ;
}
}
//后序遍历----------非递归写法,思想是:先找最左结点,找到后但不能访问最左结点,要先判断最左结点的右子树是否为空,若为空, 则可以访问最左结点,否则不可以访问最左结点,需要访问右子树。
//可以访问根结点的条件:上一层访问的节点为右子树。所以我们需要定义两个指针prev与cur ,cur用来保存当前结点,prev用来保存上一层访问的结点。
void PostOrderNonR()
{
stack<Node*> s;
Node *prev = NULL;
Node *cur = _root;
while (cur || !s.empty())
{
while (cur)//找最左结点
{
s.push(cur);
cur = cur->_left;
}
Node *top = s.top(); //定义一个栈顶指针,用来指向栈顶元素。
if (top->_right == NULL || top->_right == prev)//栈顶节点的右子树为空或者上一次访问的节点为右子树,则可以访问栈顶元素。
{
cout << top->_data << " " ;
s.pop();
prev = top;
}
else
{
cur = top->_left;
}
}
}
//二叉树的层序遍历(即是一层一层的进行遍历):思想是:需要借助队列,首先取队头,判断它是否为空,若为空直接return;不为空的时候,进行入队操作。
//如何取到队头?入数据还是入指针?最好入指针,需要保存数据或者节点的时候最好入指针。
void LevelOrder()
{
queue<Node*> q;
if (_root == NULL )
{
return;
}
q.push(_root);
while (!q.empty())
{
Node *front = q.front(); //取队头元素
q.pop();
cout << front->_data<< " ";
if (front->_left)//队头元素的左孩子不为空的时候,将它的左孩子压入队列
{
q.push(front->_left);
}
if (front->_right)//队头元素的右孩子不为空的时候,将它的右孩子压入队列
{
q.push(front->_right);
}
}
}
size_t _Depth(Node *root )//思想:当前深度=(左子树和右子树中深度较大的一个)+1;
{
if(root == NULL)
{
return 0;
}
int left = _Depth(root->_left);
int right = _Depth(root ->_right);
return left > right ? left + 1 : right + 1;
}
size_t _GetKLevel(Node *root , size_t K)//取第K层结点,递归写法。
{
if (root == NULL)
{
return 0;
}
if (K == 1)
{
return 1;
}
return _GetKLevel(root ->_left, K - 1) + _GetKLevel(root->_right, K - 1);
}
Node* _Find(Node * root, const T& x)//查找结点为x的结点
{
if (root == NULL)
{
return NULL ;
}
if (root ->_data == x)
{
return root ;
}
Node *ret = _Find( root->_left, x );
if (ret)
{
return ret;
}
else
{
return _Find(root ->_right, x);
}
}
size_t _leafsize(Node *root )//求叶子节点的个数,思想:左子树的叶子结点数目+右子树的叶子结点的数目。
{
if (root == NULL)
{
return 0;
}
if (root ->_left == NULL&& root->_right == NULL )
{
return 1;
}
return _leafsize(root ->_left) + _leafsize(root->_right);
}
//递归即是=子问题+返回条件
//方法一:
size_t _size(Node *root )//结点的数目
{
if (root == NULL)
{
return 0;
}
return _size(root ->_left) + _size(root->_right) + 1;
}
//方法二:遍历法
size_t _size(Node *root)
{
static size_t sSize = 0;//此句代码会让程序有线程安全问题
if (root == NULL )
{
return sSize;
}
++sSize;
_size(root->_left);
_size(root->_right);
return sSize;6
}
};
另外有需要云服务器可以了解下创新互联scvps.cn,海内外云服务器15元起步,三天无理由+7*72小时售后在线,公司持有idc许可证,提供“云服务器、裸金属服务器、高防服务器、香港服务器、美国服务器、虚拟主机、免备案服务器”等云主机租用服务以及企业上云的综合解决方案,具有“安全稳定、简单易用、服务可用性高、性价比高”等特点与优势,专为企业上云打造定制,能够满足用户丰富、多元化的应用场景需求。
本文标题:二叉树常考面试题-创新互联
当前地址:https://www.cdcxhl.com/article46/dddgeg.html
成都网站建设公司_创新互联,为您提供网站设计、移动网站建设、手机网站建设、网站维护、企业建站、用户体验
声明:本网站发布的内容(图片、视频和文字)以用户投稿、用户转载内容为主,如果涉及侵权请尽快告知,我们将会在第一时间删除。文章观点不代表本网站立场,如需处理请联系客服。电话:028-86922220;邮箱:631063699@qq.com。内容未经允许不得转载,或转载时需注明来源: 创新互联

- 企业网站制作优化有哪些重点 2013-11-23
- 为什么有些企业网站制作的很烂,排名还能在你前面 2014-11-17
- 企业网站制作须知:怎样建一个高端大气的网站 2013-05-15
- 企业网站制作完成后要经常更新网站内容 2021-12-09
- 北京企业网站制作完成后该如何为引流? 2023-03-23
- 企业网站制作有哪些流程?手机建站需求留心什么? 2022-07-16
- 企业网企业网站制作 2016-12-03
- 极简网页设计风格或许更适合中小企业网站制作 2020-12-16
- 企业网站制作市场需求分析! 2023-04-04
- 企业网站制作有何重要性及作用? 2022-11-12
- 企业网站制作如何选择网站空间 2021-12-04
- 企业网站制作中如何提高网站打开速度 2016-11-05