【图】（六）多源最短路径-Floyd详解-C语言-创新互联

图相关文章：
1. 图的建立 - 邻接矩阵与邻接表
2. 图的遍历 - DFS与BFS
3. 顶点度的计算
4. 最小生成树 - Prim与Kruskal
5. 单源最短路径 - Dijkstra与Bellman-Ford
6. 多源最短路径 - Floyd
7. 拓扑排序AOV网

创新互联专业为企业提供常宁网站建设、常宁做网站、常宁网站设计、常宁网站制作等企业网站建设、网页设计与制作、常宁企业网站模板建站服务，10多年常宁做网站经验，不只是建网站，更提供有价值的思路和整体网络服务。

文章目录
  • Floyd算法
    • 3.1 算法思想
      • （1）初始化
      • （2）求解
      • （3）输出
    • 3.2 实现
    • 3.3 算法分析

Floyd算法

Floyd算法是求解多源最短路径问题的典型算法，可以知道图中任意两点之间的最短路径。该算法对于有向图、无向图都适用，同时允许图中带有负权边，但是不允许有负权环。

Floyd算法采用动态规划的思想，分为多个阶段来解决问题。

若图 G G G有 n n n个顶点 ( V 0 ∼ V n − 1 ) (V_0 \sim V_{n-1}) (V0​∼Vn−1​)，则将求图中每一对顶点之间的最短路径分 n n n个阶段∶

Floyd求解过程：

  • 首先进行初始化，在没有其它顶点中转的情况下，求得各顶点间的最短路径；

  • 在各顶点间增加 V 0 V_0 V0​作为中转结点，求得各顶点间新的最短路径；

  • 再增加 V 1 V_1 V1​作为中转结点，求得各顶点间新的最短路径；

    ……

  • 最后增加 V n − 1 V_{n-1} Vn−1​作为中转结点，求得各顶点间最终的最短路径。


3.1 算法思想

Floyd只能使用邻接矩阵来实现。

为了方便理解，我们来手动模拟一下实现过程。以有向图演示，无向图同理。

我们使用两个大小为 n × n n \times n n×n的二维数组分别记录最短路径 d i s dis dis与中转顶点 p a t h path path。其中，最短路径矩阵可以告诉我们任意两顶点间的最短距离；而中转顶点矩阵可以告诉我们路径。

（1）初始化

在这里插入图片描述
初始化的最短路径矩阵其实就是邻接矩阵，中转顶点矩阵全部标记为 − 1 -1 −1，代表未经过中转。


（2）求解

① 加入 V 0 V_0 V0​中转

可以看到， V 0 V_0 V0​顶点的入度为0，所以任何顶点都不能到达 V 0 V_0 V0​，最短路径与中转顶点矩阵不变。

没有别的顶点可以通过 V 1 V_1 V1​中转或使得 d i s dis dis减少，进行下一次中转。

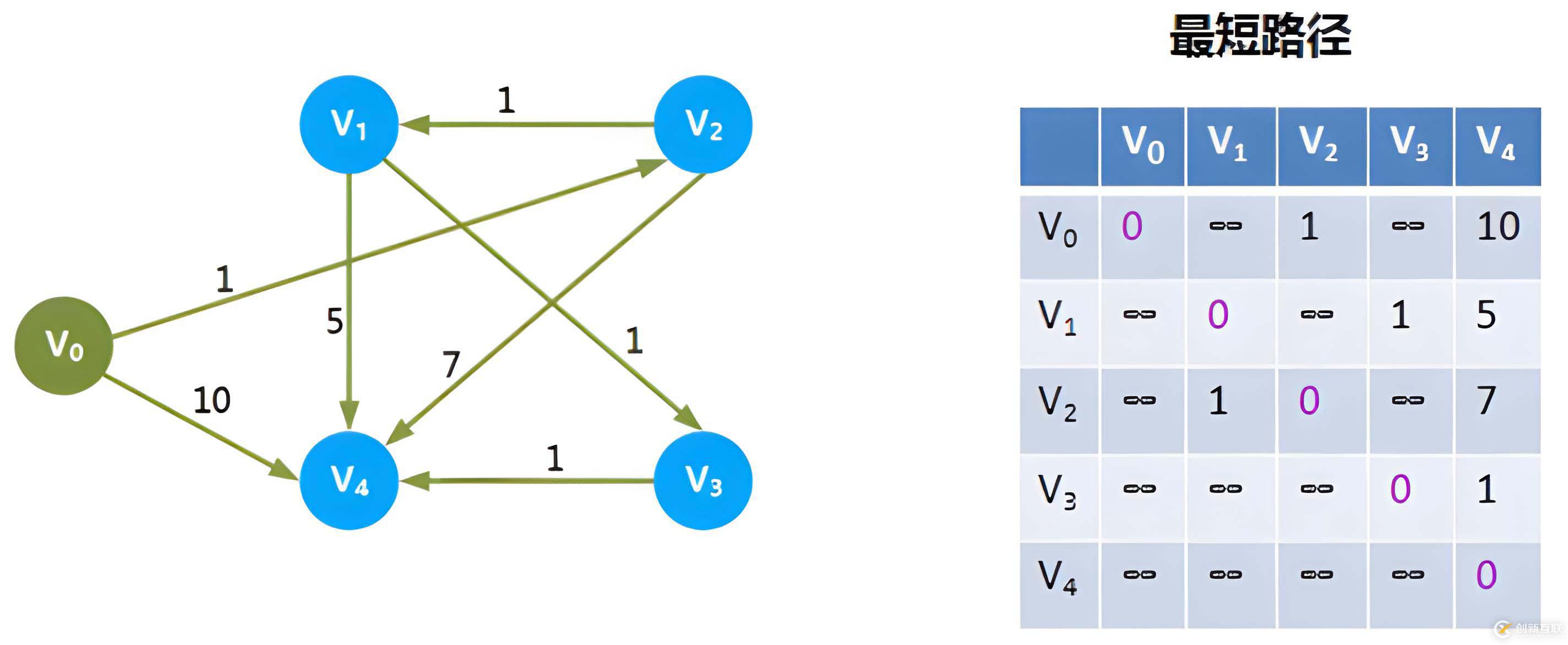
在这里插入图片描述

② 加入 V 1 V_1 V1​中转

可以看到，当我们添加到 V 1 V_1 V1​作为中转时，

原先 V 2 → V 3 = ∞ V_2 \rightarrow V_3 = \infty V2​→V3​=∞，现在 V 2 → V 1 → V 3 = 2 V_2 \rightarrow V_1 \rightarrow V_3= 2 V2​→V1​→V3​=2，更新 d i s [ V 2 ] [ V 3 ] = 2 dis[V_2][V_3]=2 dis[V2​][V3​]=2， p a t h [ V 2 ] [ V 3 ] = 1 path[V_2][V_3]=1 path[V2​][V3​]=1

原先 V 2 → V 4 = 7 V_2 \rightarrow V_4 = 7 V2​→V4​=7，现在 V 2 → V 1 → V 4 = 6 V_2 \rightarrow V_1 \rightarrow V_4= 6 V2​→V1​→V4​=6，更新 d i s [ V 2 ] [ V 4 ] = 6 dis[V_2][V_4]=6 dis[V2​][V4​]=6， p a t h [ V 2 ] [ V 4 ] = 1 path[V_2][V_4]=1 path[V2​][V4​]=1

没有别的顶点可以通过 V 1 V_1 V1​中转或使得 d i s dis dis减少，进行下一次中转。

在这里插入图片描述


③ 加入 V 2 V_2 V2​中转

可以看到，当我们添加到 V 2 V_2 V2​作为中转时，

原先 d i s [ V 0 ] [ V 1 ] = ∞ dis[V_0][V_1] = \infty dis[V0​][V1​]=∞，现在 d i s [ V 0 ] [ V 2 ] + d i s [ V 2 ] [ V 1 ] = 2 dis[V_0][V_2] + dis[V_2][V_1]= 2 dis[V0​][V2​]+dis[V2​][V1​]=2，更新 d i s [ V 0 ] [ V 1 ] = 2 dis[V_0][V_1]=2 dis[V0​][V1​]=2， p a t h [ V 0 ] [ V 1 ] = 2 path[V_0][V_1]=2 path[V0​][V1​]=2

原先 d i s [ V 0 ] [ V 3 ] = ∞ dis[V_0][V_3] = \infty dis[V0​][V3​]=∞，现在 d i s [ V 0 ] [ V 2 ] + d i s [ V 2 ] [ V 3 ] = 3 dis[V_0][V_2] + dis[V_2][V_3]= 3 dis[V0​][V2​]+dis[V2​][V3​]=3，更新 d i s [ V 0 ] [ V 3 ] = 3 dis[V_0][V_3]=3 dis[V0​][V3​]=3， p a t h [ V 0 ] [ V 3 ] = 2 path[V_0][V_3]=2 path[V0​][V3​]=2

原先 d i s [ V 0 ] [ V 4 ] = 10 dis[V_0][V_4] = 10 dis[V0​][V4​]=10，现在 d i s [ V 0 ] [ V 2 ] + d i s [ V 2 ] [ V 4 ] = 7 dis[V_0][V_2] + dis[V_2][V_4]= 7 dis[V0​][V2​]+dis[V2​][V4​]=7，更新 d i s [ V 0 ] [ V 4 ] = 7 dis[V_0][V_4]=7 dis[V0​][V4​]=7， p a t h [ V 0 ] [ V 4 ] = 2 path[V_0][V_4]=2 path[V0​][V4​]=2

没有别的顶点可以通过 V 2 V_2 V2​中转或使得 d i s dis dis减少，进行下一次中转。

在这里插入图片描述


④ 加入 V 3 V_3 V3​中转

可以看到，当我们添加到 V 3 V_3 V3​作为中转时，

原先 d i s [ V 0 ] [ V 4 ] = 7 dis[V_0][V_4] = 7 dis[V0​][V4​]=7，现在 d i s [ V 0 ] [ V 3 ] + d i s [ V 3 ] [ V 4 ] = 4 dis[V_0][V_3] + dis[V_3][V_4]= 4 dis[V0​][V3​]+dis[V3​][V4​]=4，更新 d i s [ V 0 ] [ V 4 ] = 4 dis[V_0][V_4]= 4 dis[V0​][V4​]=4， p a t h [ V 0 ] [ V 4 ] = 3 path[V_0][V_4]=3 path[V0​][V4​]=3

原先 d i s [ V 1 ] [ V 4 ] = 5 dis[V_1][V_4] = 5 dis[V1​][V4​]=5，现在 d i s [ V 1 ] [ V 3 ] + d i s [ V 3 ] [ V 4 ] = 2 dis[V_1][V_3] + dis[V_3][V_4]= 2 dis[V1​][V3​]+dis[V3​][V4​]=2，更新 d i s [ V 1 ] [ V 4 ] = 2 dis[V_1][V_4]=2 dis[V1​][V4​]=2， p a t h [ V 1 ] [ V 4 ] = 3 path[V_1][V_4]=3 path[V1​][V4​]=3

原先 d i s [ V 2 ] [ V 4 ] = 6 dis[V_2][V_4] = 6 dis[V2​][V4​]=6，现在 d i s [ V 2 ] [ V 3 ] + d i s [ V 3 ] [ V 4 ] = 3 dis[V_2][V_3] + dis[V_3][V_4]= 3 dis[V2​][V3​]+dis[V3​][V4​]=3，更新 d i s [ V 2 ] [ V 4 ] = 3 dis[V_2][V_4]=3 dis[V2​][V4​]=3， p a t h [ V 1 ] [ V 4 ] = 3 path[V_1][V_4]=3 path[V1​][V4​]=3

没有别的顶点可以通过 V 3 V_3 V3​中转或使得 d i s dis dis减少，进行下一次中转。

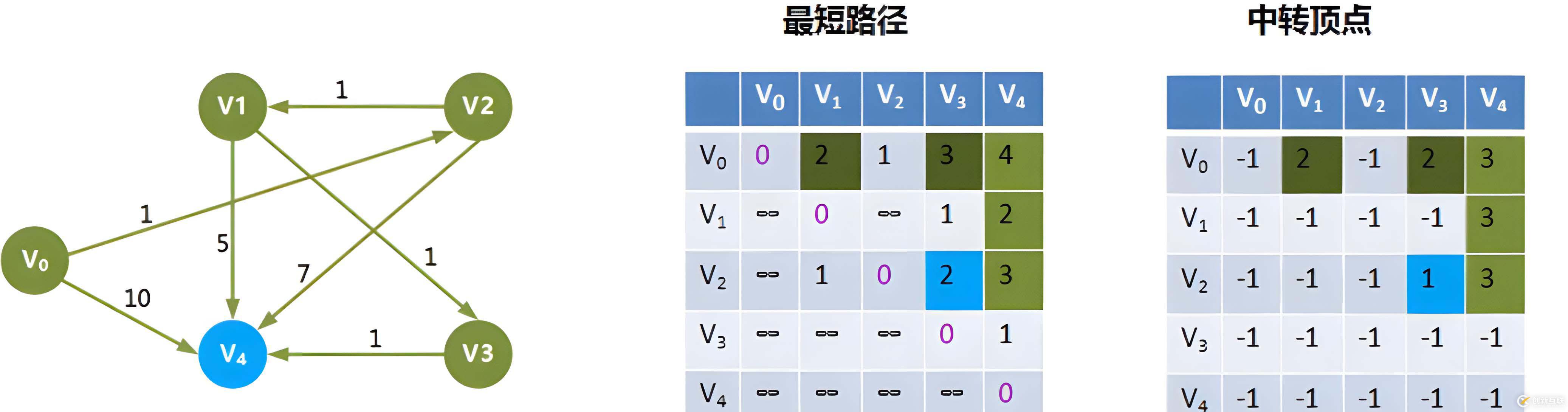
在这里插入图片描述


⑤ 加入 V 4 V_4 V4​中转

可以看到，当我们添加到 V 4 V_4 V4​作为中转时，由于 V 4 V_4 V4​的出度为0，故不会进行更新，且已经将所有顶点中转完成，得到的便是最终结果。

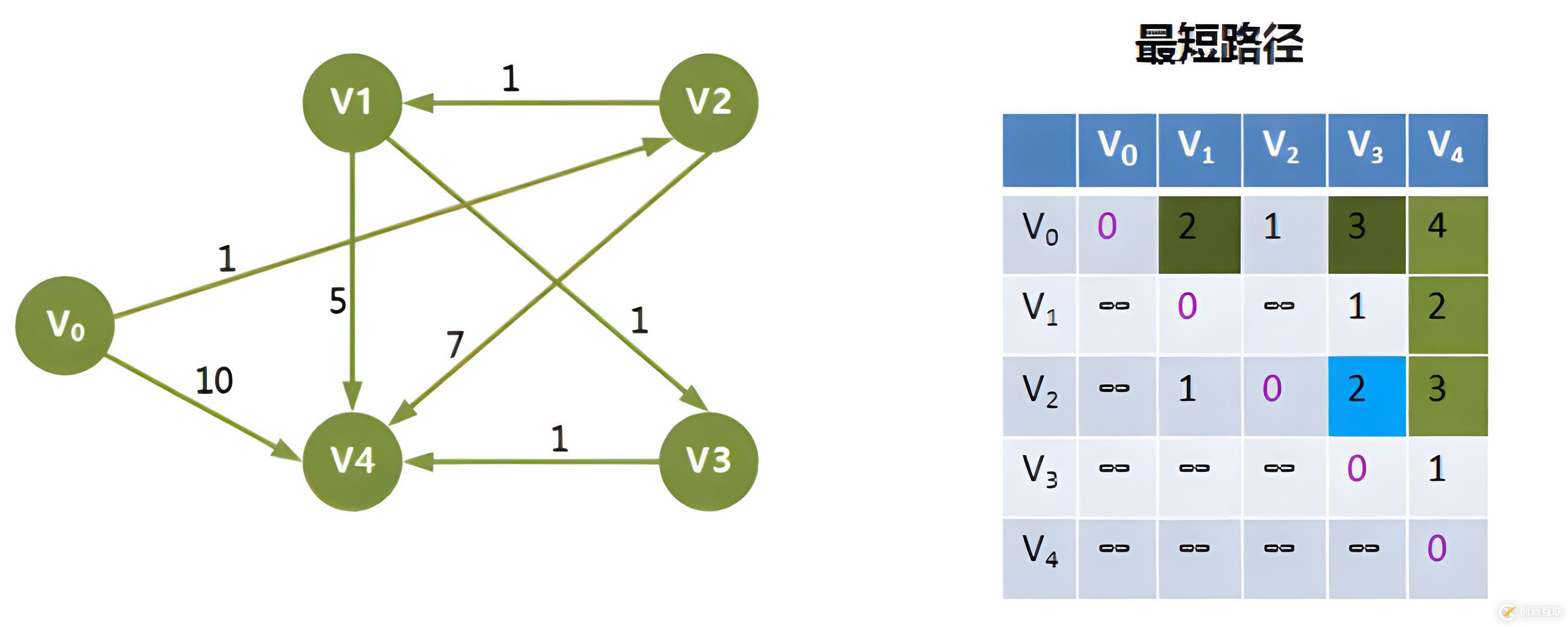
在这里插入图片描述

（3）输出

d i s [ i ] [ j ] dis[i][j] dis[i][j]存储的便是 V i ∼ V j V_i \sim V_j Vi​∼Vj​的最短路径长度。

而想要输出 V i ∼ V j V_i \sim V_j Vi​∼Vj​的最短路径，则需要顺着 p a t h path path数组往前找。

以上图的 V 2 ∼ V 4 V_2 \sim V_4 V2​∼V4​顶点为例：

首先 p a t h [ V 2 ] [ V 4 ] = 3 path[V_2][V_4]=3 path[V2​][V4​]=3，则说明经过 V 3 V_3 V3​进行中转，路径为 V 2 → ( V 3 ) → V 4 V_2 \rightarrow (V_3) \rightarrow V_4 V2​→(V3​)→V4​

接着找 p a t h [ V 2 ] [ V 3 ] = 1 path[V_2][V_3]=1 path[V2​][V3​]=1，则说明经过 V 1 V_1 V1​进行中转，路径为 V 2 → ( V 1 ) → V 3 → V 4 V_2 \rightarrow (V_1) \rightarrow V_3 \rightarrow V_4 V2​→(V1​)→V3​→V4​

接着找 p a t h [ V 2 ] [ V 1 ] = − 1 path[V_2][V_1]=-1 path[V2​][V1​]=−1，则说明没有经过任何顶点进行中转，得到最终的路径为 V 2 → V 1 → V 3 → V 4 V_2 \rightarrow V_1 \rightarrow V_3 \rightarrow V_4 V2​→V1​→V3​→V4​


3.2 实现

给出核心部分的C语言代码：

for (k = 0; k< VertexNum; k++) // 将每个顶点都作为中转尝试
{// 遍历整个矩阵 i-行 j-列
    for (i = 0; i< VertexNum; i++)
    {for (j = 0; j< VertexNum; j++)
        {// 若经过k顶点中转，路径更短，则更新矩阵
            if (dis[i][k] + dis[k][j]< dis[i][j])
            {dis[i][j] = dis[i][k] + dis[k][j]; // 更新dis矩阵
                path[i][j] = k;                    // 更新path矩阵
            }
        }
    }
}

3.3 算法分析

  • 空间复杂度 O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2)

  • 时间复杂度 O ( ∣ V ∣ 3 ) O(|V|^3) O(∣V∣3)

估计这时候你也看出了一些问题，我使用Dijkstra算法将每个顶点作为起点计算一遍，时间复杂度不也是 O ( ∣ V ∣ 3 ) O(|V|^3) O(∣V∣3)吗？那Floyd算法的优势在哪里呢？

其实，虽然两种算法都是 O ( ∣ V ∣ 3 ) O(|V|^3) O(∣V∣3)，但是前面的系数并不相同，Floyd的系数会更小一些，所有效率也会更高一些。也因此，即使它的复杂度到达了 O ( ∣ V ∣ 3 ) O(|V|^3) O(∣V∣3)的程度，对于一些中小规模的图仍然是适用的。

同时Floyd也支持负权边，也是其一个优点。

你是否还在寻找稳定的海外服务器提供商？创新互联www.cdcxhl.cn海外机房具备T级流量清洗系统配攻击溯源，准确流量调度确保服务器高可用性，企业级服务器适合批量采购，新人活动首月15元起，快前往官网查看详情吧

文章题目：【图】（六）多源最短路径-Floyd详解-C语言-创新互联
当前地址：https://www.cdcxhl.com/article42/dshjhc.html

成都网站建设公司_创新互联，为您提供搜索引擎优化、做网站、网页设计公司、品牌网站建设、品牌网站设计、电子商务

广告

声明：本网站发布的内容（图片、视频和文字）以用户投稿、用户转载内容为主，如果涉及侵权请尽快告知，我们将会在第一时间删除。文章观点不代表本网站立场，如需处理请联系客服。电话：028-86922220；邮箱：631063699@qq.com。内容未经允许不得转载，或转载时需注明来源： 创新互联

猜你还喜欢下面的内容

成都网站建设公司

网站维护知识

分类信息网