【蓝桥杯】历届真题杨辉三角形(省赛)Java-创新互联
【问题描述】

下面的图形是著名的杨辉三角形:
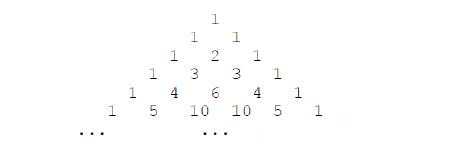
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列:
1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,...
给定一个正整数N,请你输出数列中第一次出现Ⅳ是在第几个数?
【输入格式】
输入一个整数N。
【输出格式】
输出一个整数代表答案。
【样例输入】
6
【样例输出】
13

【思路与分析】
首先,要新建一个数组以存放杨辉三角中的值。该长度通过题目中所给出的图示进行计算,此时有一个小窍门。通过观察可知杨辉三角左右半边的值为相同的,或者说杨辉三角是中心对称的。因此,可以先从中间一分为二,选取左半边或右半边进行计算。
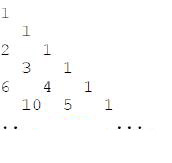
经过观察,不难总结出规律:y = x * (x-1) / 2
后续计算同样基于该规律所做。
【代码】
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
long N= sc.nextLong();
//经过计算在第44721行的时候,第三列的值将会超过十亿
//所以我们创建44725长度的数组
long[] a=new long[44725];
a[0]=1L; //将数组0位置存入一个长整形
if(N==1) { //当N==1,直接输出1
System.out.println(1);
return;
}
//声明一个标志位
int count=1;
for(int i=1;i<44725;i++) {
for(int j=i;j>=1;j--) {
//按照杨辉三角的数字规律填充数组
a[j]=a[j]+a[j-1];
//找到了N,则输出当前位置,位置 的计算等于 前面的个数 + 当行的位置数
if(a[j]==N) {
//前面的个数 = (count+1)*count/2 ,当行的个数 = i-j+1
System.out.println((count+1)*count/2+i-j+1);
return;
}
}
//判断完后,标志位++
count++;
}
//这是未找到的情况,就是说有些小于10亿的数在44721行之前都还没有出现 ,
//那么它必然是出现在未显示出来的第二列的位置上
System.out.println((N+1)*N/2+2);
//所以 位置 = 前面出现的个数 + 2
}
}【Q&A】
为什么在for循环中不使用 break 而使用return?
答:return在for循环中的作用为:返回return所返回的值,并不会执行下一次循环。因不能干扰count标志位的运算,因此 使用return代替break。若使用break,在OJ测试时将只有60分,无法拿到满分。
为什么在存入数组元素时使用 1L 而不是 1?
答:L表示long ,long占用8个字节,表示范围:-9223372036854775808 ~ 9223372036854775807
1L其实就是1。
后面跟L一般是指数据类型,1L表示1是长整型,如果是1f 表示是float型,若是1 则表示 int 型。
你是否还在寻找稳定的海外服务器提供商?创新互联www.cdcxhl.cn海外机房具备T级流量清洗系统配攻击溯源,准确流量调度确保服务器高可用性,企业级服务器适合批量采购,新人活动首月15元起,快前往官网查看详情吧
网站题目:【蓝桥杯】历届真题杨辉三角形(省赛)Java-创新互联
URL网址:https://www.cdcxhl.com/article38/hodsp.html
成都网站建设公司_创新互联,为您提供网站改版、网站排名、定制开发、品牌网站建设、外贸网站建设、网站设计
声明:本网站发布的内容(图片、视频和文字)以用户投稿、用户转载内容为主,如果涉及侵权请尽快告知,我们将会在第一时间删除。文章观点不代表本网站立场,如需处理请联系客服。电话:028-86922220;邮箱:631063699@qq.com。内容未经允许不得转载,或转载时需注明来源: 创新互联

- 新顶级域名注册去哪儿? 2022-07-15
- 域名注册证书怎么弄?有什么用 2021-03-01
- 国内域名注册条件和选择原则是什么? 2016-11-18
- 如何保护注册域名?保护域名不被别人抢注 2017-03-10
- 用域名注册量来画地图,你见过吗? 2021-03-05
- 企业网站建设注册域名的重要性 2016-11-09
- 域名注册与域名解析 2016-08-31
- 注册域名需要注意什么事项 2014-07-24
- 网站建设国际域名注册要求 2021-04-25
- 佛山网站制作中域名注册的问题 2022-11-30
- 关于网站域名注册和国际国内域名的问题解答 2022-08-15
- 注册域名和备案所需资料摘要 2016-12-21