python和c++怎么实现旋转矩阵到欧拉角的变换方式-创新互联

这篇文章给大家分享的是有关python和c++怎么实现旋转矩阵到欧拉角的变换方式的内容。小编觉得挺实用的，因此分享给大家做个参考，一起跟随小编过来看看吧。

创新互联公司专注于企业营销型网站建设、网站重做改版、义马网站定制设计、自适应品牌网站建设、成都h5网站建设、商城系统网站开发、集团公司官网建设、外贸营销网站建设、高端网站制作、响应式网页设计等建站业务，价格优惠性价比高，为义马等各大城市提供网站开发制作服务。

在摄影测量学科中，国际摄影测量遵循OPK系统，即是xyz转角系统，而工业中往往使用zyx转角系统。

旋转矩阵的意义：描述相对地面的旋转情况，yaw-pitch-roll对应zyx对应k,p,w

#include <iostream>
#include<stdlib.h>
#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Dense>
#include<stdlib.h>
using namespace std;
Eigen::Matrix3d rotationVectorToMatrix(Eigen::Vector3d theta)
{
  Eigen::Matrix3d R_x=Eigen::AngleAxisd(theta(0),Eigen::Vector3d(1,0,0)).toRotationMatrix();
  Eigen::Matrix3d R_y=Eigen::AngleAxisd(theta(1),Eigen::Vector3d(0,1,0)).toRotationMatrix();
  Eigen::Matrix3d R_z=Eigen::AngleAxisd(theta(2),Eigen::Vector3d(0,0,1)).toRotationMatrix();
  return R_z*R_y*R_x;

}
bool isRotationMatirx(Eigen::Matrix3d R)
{
  int err=1e-6;//判断R是否奇异
  Eigen::Matrix3d shouldIdenity;
  shouldIdenity=R*R.transpose();
  Eigen::Matrix3d I=Eigen::Matrix3d::Identity();
  return (shouldIdenity-I).norm()<err?true:false;
}

int main(int argc, char *argv[])
{
  Eigen::Matrix3d R;
  Eigen::Vector3d theta(rand() % 360 - 180.0, rand() % 360 - 180.0, rand() % 360 - 180.0);
  theta=theta*M_PI/180;
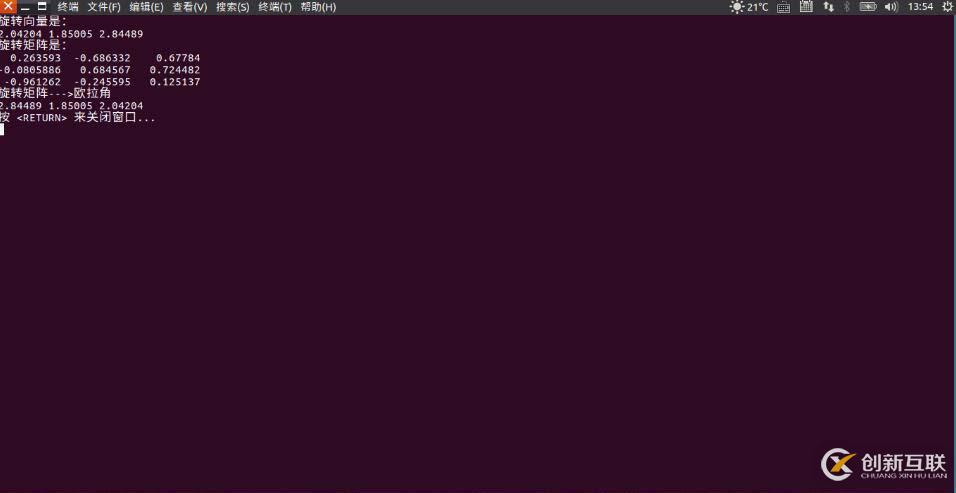
  cout<<"旋转向量是：\n"<<theta.transpose()<<endl;
  R=rotationVectorToMatrix(theta);
  cout<<"旋转矩阵是：\n"<<R<<endl;
  if(! isRotationMatirx(R)){
   cout<<"旋转矩阵--->欧拉角\n"<<R.eulerAngles(2,1,0).transpose()<<endl;//z-y-x顺序，与theta顺序是x,y,z
  }
  else{
    assert(isRotationMatirx(R));
  }

  return 0;
}

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

import cv2
import numpy as np
import math
import random

def isRotationMatrix(R) :
  Rt = np.transpose(R)
  shouldBeIdentity = np.dot(Rt, R)
  I = np.identity(3, dtype = R.dtype)
  n = np.linalg.norm(I - shouldBeIdentity)
  return n < 1e-6

def rotationMatrixToEulerAngles(R) :

  assert(isRotationMatrix(R))
  
  sy = math.sqrt(R[0,0] * R[0,0] + R[1,0] * R[1,0])
  
  singular = sy < 1e-6

  if not singular :
    x = math.atan2(R[2,1] , R[2,2])
    y = math.atan2(-R[2,0], sy)
    z = math.atan2(R[1,0], R[0,0])
  else :
    x = math.atan2(-R[1,2], R[1,1])
    y = math.atan2(-R[2,0], sy)
    z = 0

  return np.array([x, y, z])

def eulerAnglesToRotationMatrix(theta) :
  
  R_x = np.array([[1,     0,         0          ],
          [0,     math.cos(theta[0]), -math.sin(theta[0]) ],
          [0,     math.sin(theta[0]), math.cos(theta[0]) ]
          ])
    
    
          
  R_y = np.array([[math.cos(theta[1]),  0,   math.sin(theta[1]) ],
          [0,           1,   0          ],
          [-math.sin(theta[1]),  0,   math.cos(theta[1]) ]
          ])
        
  R_z = np.array([[math.cos(theta[2]),  -math.sin(theta[2]),  0],
          [math.sin(theta[2]),  math.cos(theta[2]),   0],
          [0,           0,           1]
          ])
          
          
  R = np.dot(R_z, np.dot( R_y, R_x ))

  return R


if __name__ == '__main__' :

  e = np.random.rand(3) * math.pi * 2 - math.pi
  
  R = eulerAnglesToRotationMatrix(e)
  e1 = rotationMatrixToEulerAngles(R)

  R1 = eulerAnglesToRotationMatrix(e1)
  print ("\nInput Euler angles :\n{0}".format(e))
  print ("\nR :\n{0}".format(R))
  print ("\nOutput Euler angles :\n{0}".format(e1))
  print ("\nR1 :\n{0}".format(R1))

感谢各位的阅读！关于“python和c++怎么实现旋转矩阵到欧拉角的变换方式”这篇文章就分享到这里了，希望以上内容可以对大家有一定的帮助，让大家可以学到更多知识，如果觉得文章不错，可以把它分享出去让更多的人看到吧！

另外有需要云服务器可以了解下创新互联scvps.cn，海内外云服务器15元起步，三天无理由+7*72小时售后在线，公司持有idc许可证，提供“云服务器、裸金属服务器、高防服务器、香港服务器、美国服务器、虚拟主机、免备案服务器”等云主机租用服务以及企业上云的综合解决方案，具有“安全稳定、简单易用、服务可用性高、性价比高”等特点与优势，专为企业上云打造定制，能够满足用户丰富、多元化的应用场景需求。

网站题目：python和c++怎么实现旋转矩阵到欧拉角的变换方式-创新互联
转载来于：https://www.cdcxhl.com/article34/docspe.html

成都网站建设公司_创新互联，为您提供商城网站、微信公众号、App开发、移动网站建设、建站公司、品牌网站制作

广告

声明：本网站发布的内容（图片、视频和文字）以用户投稿、用户转载内容为主，如果涉及侵权请尽快告知，我们将会在第一时间删除。文章观点不代表本网站立场，如需处理请联系客服。电话：028-86922220；邮箱：631063699@qq.com。内容未经允许不得转载，或转载时需注明来源： 创新互联