python中计算pi的方法-创新互联

创新互联www.cdcxhl.cn八线动态BGP香港云服务器提供商，新人活动买多久送多久，划算不套路！

为筠连等地区用户提供了全套网页设计制作服务，及筠连网站建设行业解决方案。主营业务为网站设计制作、网站设计、筠连网站设计，以传统方式定制建设网站，并提供域名空间备案等一条龙服务，秉承以专业、用心的态度为用户提供真诚的服务。我们深信只要达到每一位用户的要求，就会得到认可，从而选择与我们长期合作。这样，我们也可以走得更远！

小编给大家分享一下python中计算pi的方法，相信大部分人都还不怎么了解，因此分享这篇文章给大家参考一下，希望大家阅读完这篇文章后大有收获，下面让我们一起去了解一下吧！

一、π的简介

π的介绍

圆周率用希腊字母 π（读作pài）表示，是一个常数（约等于3.141592654），是代表圆周长和直径的比值。它是一个即无限不循环小数，在日常生活中，通常都用3.14代表圆周率去进行近似计算。

π的求解历程

1965年，英国数学家约翰·沃利斯（John Wallis）出版了一本数学专著，其中他推导出一个公式，发现圆周率等于无穷个分数相乘的积。

2015年，罗切斯特大学的科学家们在氢原子能级的量子力学计算中发现了圆周率相同的公式。

2019年3月14日，谷歌宣布圆周率现已到小数点后31.4万亿位。

二、π的近似计算

1 计算公式

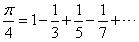
python中计算pi的方法

2. 方法讲解

所用公式等式右边分子都为1，分母为递增数列，从第一项开始，奇数项符号为正，偶数项符号为负。等式右边的分母越大，越小，圆周率π计算的值越精确；换个角度讲，就是等式右边的项越多，计算的值越精确。

3. 代码实现(python)

from math import fabs        #导入数学模块
from time import perf_counter   #导入时间模块

    def Bar(i):         #动态文本条
        N = pow(10,level)
        a = int((i/N)*50)
        b = 50 - a
        Y , N = '*' * a , '.' * b
   print("\r计算中：{:3.0f}% [{}->{}] {:.2f}s".format(2*a,Y,N,perf_counter()),end='')
     
level = eval(input('计算Pi精确到小数点后几位数：'))
print('\n{:=^70}'.format('计算开始'))
a,b,pi,tmp = 1,1,0,1
i = 0
'''
a 分子  |  b 分母  |  pi 圆周率
tmp 存储a/b的值    |  i  执行进度
'''
perf_counter()      #开始计时
while (fabs(tmp) >= pow(10,-level)): #计算Pi
    pi += tmp
    b += 2
    a = -a
    tmp = a/b
    i += 2
    Bar(i)          #调用函数，实时显示计算进度

print('\n{:=^70}'.format('计算完成'))
print('\nPi的计算值为：{}'.format(round(pi*4,level))) #输出计算结果

4. 图片示例

python中计算pi的方法